Une étude d’intervention a pour but d’évaluer si un traitement donné montre, versus traitement de référence ou placebo, un effet clinique pertinent. Pour assurer une fiabilité statistique à ce résultat, il faut que l’étude repose sur un échantillon suffisant de la population cible du traitement.

Calcul de la taille d’échantillon pour une étude

L’approche conventionnelle du calcul de l’échantillon de population nécessaire pour une étude repose sur quatre éléments (1) : l’erreur de type I, la puissance d’étude, les suppositions dans le groupe contrôle pour la fréquence de réponse et la variabilité de celle-ci, et, enfin, l’effet attendu pour le traitement.

L’erreur de type I (erreur alpha) consiste, dans une étude de supériorité d’un traitement versus un autre, à rejeter à tort l’hypothèse nulle (absence de différence) c’est-à-dire de conclure à tort qu’une différence existe entre les 2 traitements. Par convention, un risque de 5% est accepté, soit une valeur p > 0,05.

L’erreur de type II (erreur bêta) consiste à accepter, dans le même cadre, à tort l’hypothèse nulle, c’est-à-dire de conclure qu’il n’existe pas de différence entre les 2 traitements alors qu’il en existe une. En pratique statistique, le terme de puissance est utilisé pour désigner le nombre de patients nécessaires à inclure pour éviter cette erreur de type II. Par convention, elle est généralement fixée à au moins 80%.

Les suppositions de survenue d’événements dans le groupe contrôle reposent souvent sur une estimation dans une étude pilote dans la population cible de patients. Pour le calcul de l’échantillon, c’est la variance des résultats qui est utilisée, indicateur de la dispersion des résultats. Se baser sur une étude pilote fait cependant l’objet de nombreuses critiques, pour son manque de fiabilité. Des alternatives sont proposées : utiliser une autre formule de calcul basée sur une différence minimale cliniquement importante ou prendre comme repère une envergure de l’intervalle de confiance ne dépassant pas une valeur préspécifée (2).

L’effet attendu du traitement est la différence minimale supposée détectable entre les deux traitements, cliniquement importante/pertinente. Ce sont ces deux derniers éléments précités qui comportent le plus d’incertitudes qui peuvent conduire à diminuer la puissance de l’étude.

Sur base de ces 4 éléments, la taille d’échantillon peut être calculée au moyen d’une formule mathématique (2) ou grâce à un nomogramme de Gore et Altman (3).

Le calcul d’une puissance post hoc n’apporte pas d’élément utile pour la clinique ; à ce stade, ce sont les intervalles de confiance des résultats qui apporteront les renseignements les plus pertinents (2). L’envergure de l’intervalle de confiance est inversement proportionnelle au nombre de sujets inclus. Un intervalle de confiance plus étroit augmente la précision d’un résultat, ce qui est parfois un élément déterminant pour montrer une différence significative, non montrée en cas d’échantillon insuffisant.

Illustration

Exemple (d’après 3 remanié)

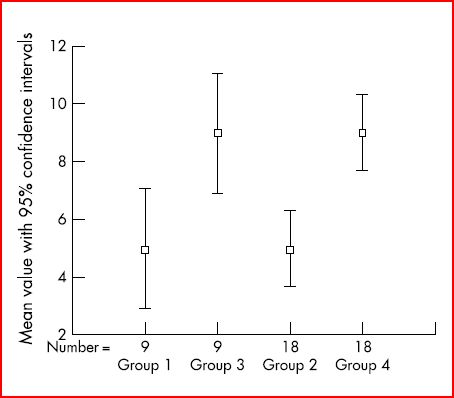
Résultats d’une évaluation d’un traitement dans 4 groupes différents

Groupes 1 et 3 : 9 participants dans chaque groupe, résultats en partie différents dans les 2 groupes, donc avec moyennes différentes, mais recouvrement des intervalles de confiance entre ces 2 groupes = pas de différence statistiquement significative.

Groupes 2 et 4 : 18 participants dans chaque groupe ; mêmes valeurs moyennes obtenues pour les participants pour le groupe 2 versus groupe 1 et pour le groupe 4 versus groupe 3 ; avec chaque fois 2 participants ayant les mêmes résultats qu’un participant des groupes 1 et 3 ; il n’y a plus de recouvrement des intervalles de confiance = différence statistiquement significative.

Cet exemple montre qu’en augmentant la taille de l’échantillon, il n’y a plus de chevauchement des intervalles de confiance des 2 groupes (= différence peut-être liée au hasard) et qu’une différence statistiquement significative est montrée.

Informations mentionnées dans les publications

Les publications d’étude permettent-elles de vérifier si le calcul d’échantillon a été correctement réalisé lors de l’élaboration du protocole d’étude ? Une revue récente (1) des études de supériorité randomisées avec un unique critère de jugement primaire publiées en 2005-2006 dans 6 revues médicales à « impact factor » élevé montre des résultats fort préoccupants. Sur les 215 articles sélectionnés, 5% ne mentionnent pas de calcul d’échantillon, 43% ne donnent pas de renseignement sur tous les critères requis. Plus de 10 % de différences sont constatés entre les calculs d’échantillon donnés dans l’article et un nouveau calcul effectué par les auteurs de cette recherche dans la littérature qui n’ont cependant trouvé les données nécessaires pour ce recalcul que dans environ 30% des études. Ces auteurs précisent aussi des différences de plus de 30% entre les données observées dans le groupe contrôle et les données initialement supposées dans 31% des études et une différence de plus de 50% dans 17% des cas. Au total seuls 34% des études fournissent toutes les données pour le recalcul de la taille d’échantillon, des calculs exacts et des suppositions exactes pour le groupe contrôle. Les auteurs concluent sur un questionnement à propos de la méthodologie de calcul de la taille de l’échantillon dans les RCTs.

Conclusion

Les règles pour le calcul de la taille d’un échantillon dans une étude sont bien codifiées. Leur bonne application est cependant impossible à vérifier dans la majorité des RCTs publiées dans les revues de grand renom.

Références

1. Charles P, Giraudeau B, Dechartres A, et al. Reporting of sample size calculation in randomised controlled trials: review. BMJ 2009;338:b1732.
2. Brasher PMA, Brant FB. Sample size calculations in randomized trials: common pitfalls. Can J Anesth 2007;54:103-6.
3. Jones SR, Carley S, Harrison M. An introduction to power and sample size estimation. Emerg Med J 2003;20:453-8.