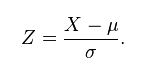Une récente étude clinique randomisée menée auprès de personnes âgées atteintes d’altération des fonctions cognitives a voulu examiner l’effet d’une intervention à plusieurs composantes sur les fonctions cognitives (1). Pour ce faire, les investigateurs ont utilisé la batterie de tests neuropsychologiques NTB (Neuropsychological Test Battery ou MTB - Mental Test Battery) immédiatement après randomisation et à 12 mois et 24 mois de suivi. La NTB comporte 14 tests qui utilisent chacun des échelles différentes. Il est donc impossible de sommer les différents scores. Un score global ne sera par conséquent possible que si les différents scores sont préalablement standardisés.

Le score z d’une valeur mesurée est le nombre d’écarts-types (déviations standard) qui séparent cette valeur de la valeur moyenne attendue dans la population. Le score z peut donc se calculer à partir de la valeur mesurée X, de la moyenne μ de la population et de l’écart-type σ de la population. (2)

 

 

 

Pour une variable déterminée, il est ainsi possible de situer chaque personne par rapport à la moyenne de la population. La moyenne peut éventuellement être estimée à partir d’un échantillon. Plus une personne est éloignée de la moyenne, plus la valeur du score z est élevée. Le signe positif ou négatif indique si la personne se situe respectivement au-dessus ou en dessous de la moyenne. Si la variable suit une répartition normale dans la population, 68% des personnes auront un score z entre -1 et +1, 95% entre -2 et +2, et 99,7% entre -3 et +3 écarts-types par rapport à la moyenne. Les personnes ayant un score z supérieur à +3 ou inférieur à -3 peuvent être considérées comme exceptionnelles.

Une conséquence intéressante du fait que les valeurs mesurées sont réparties en fonction de l’écart-type est que, de ce fait, l’unité de mesure de la variable disparaît. Par conséquent, il devient possible de comparer entre elles différentes variables en fonction de leurs scores z et éventuellement de les additionner.

Pour revenir à notre exemple, le score z a été calculé pour chaque composante de la NTB, tant pour le groupe intervention que pour le groupe témoin, en utilisant la moyenne et l’écart-type de tous les participants chez qui une valeur était connue en début d’étude. Ensuite, le score z moyen pour la NTB a été calculé dans le groupe intervention et dans le groupe témoin afin de les comparer.

 

Conclusion

Le score z ou z-score est un score donnant le nombre d’écarts-type entre la valeur mesurée et la valeur moyenne dans le groupe d’âge concerné. Ce nombre n’a pas de dimension. Cette méthode peut permettre de mieux comparer différentes variables et éventuellement de les additionner.

 

 

Références 

1. Vermeulen B. Intervention à composantes multiples en cas de risque de démence chez la personne âgée ? MinervaF 2015;14(8):100-1.
2. Sedgwick P. Standardisation of outcome measures (z-scores). BMJ 2012;345:e6178.