---

Het verband of de associatie tussen twee of meerdere variabelen kan men uitdrukken met regressie en correlatie, twee termen die vaak met elkaar verward worden (1).

Wanneer een scatterplot suggereert dat de gegevens van twee variabelen gelijkmatig veranderen, kunnen we  met behulp van een lineaire regressieanalyse bepalen welke rechte lijn deze gelijkmatige verandering het best kan benaderen. Grafisch komt het erop neer dat we zoeken naar de lijn waarbij de afstand van alle punten tot deze lijn zo klein mogelijk gehouden wordt (zie figuur 1). Wiskundig kunnen we deze regressielijn uitdrukken met de formule (2):   

waarde van afhankelijke variabele = intercept + regressiecoëfficiënt ß x waarde van onafhankelijke variabele

 

De regressiecoëfficiënt ß geeft aan in welke mate de waarde van een afhankelijke variabele gemiddeld zal veranderen wanneer de waarde van de onafhankelijke (of voorspellende of verklarende) variabele verandert. De waarde van de intercept kan men bepalen door de onafhankelijke variabele de waarde nul te geven (zie figuur 1).

 

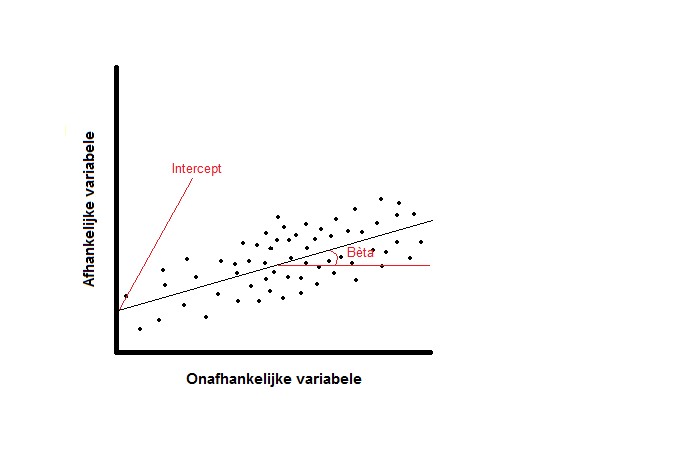
Figuur 1: Scatterplot met regressielijn.

 

Voorbeeld:

In de studie van Little (3,4) wou men nagaan in welke mate de tevredenheid van de patiënt (de MISS-score) (=afhankelijke variabele) toenam of afnam naargelang het aantal gebaren de arts maakte (=onafhankelijke of voorspellende variabele). De lineaire regressieanalyse toonde een positieve associatie tussen beide variabelen met een (univariate) regressiecoëfficiënt van 0,11 en een 95% betrouwbaarheidsinterval van 0,02 tot 0,19 (en een p-waarde van 0,018). Voor elk extra gebaar van de arts nam de MISS-score dus gemiddeld met 0,11 punten toe op een schaal van 1 tot 7. Door het brede betrouwbaarheidsinterval kan deze toename in werkelijkheid echter slechts 0,02 punten of eerder 0,19 punten bedragen.

Vaak is het zo dat men het verband zoekt tussen een afhankelijke variabele en meerdere onafhankelijke variabelen. Met een multipele regressieanalyse kunnen we dan voor elke onafhankelijke variabele een partiële regressiecoëfficiënt berekenen (5). De wiskundige formule van de regressie zal er dan als volgt uitzien:

waarde van afhankelijke variabele = intercept + regressiecoëfficiënt ß1 x waarde van onafhankelijke variabele1 + regressiecoëfficiënt ß2 x waarde van onafhankelijke variabele2 + … + regressiecoëfficiënt ßn x waarde van onafhankelijke variabelen

 

Zo is in ons voorbeeld (3,4) de (multivariate) regressiecoëfficiënt 0,08 (met 95% BI van 0,01 tot 0,15 en p-waarde van 0,046). Hieruit blijkt dus dat we de tevredenheid van de patiënt iets minder goed kunnen voorspellen op basis van het aantal gebaren dat de arts maakt als we ook met andere onafhankelijke variabelen rekening houden.

Een univariate regressieanalyse geeft ons een idee hoe twee variabelen met elkaar geassocieerd zijn, maar laat niet toe om te bepalen hoe sterk deze associatie is. De sterkte van de associatie wordt uitgedrukt met de correlatiecoëfficiënt r, een getal dat steeds tussen -1 (perfect lineair verband met negatieve helling) en +1 (perfect lineair verband met positieve helling) ligt en geen onderscheid maakt tussen afhankelijke en onafhankelijke variabelen (6). Dit getal zal dus afhankelijk zijn van de spreiding van de verschillende gegevens rond de regressielijn. In figuur 2 en 3 zien we twee scatterplots met eenzelfde regressielijn. Door de zwakke correlatie tussen de variabelen in figuur 2 zal de hellingshoek (regressiecoëfficiënt ß) een breed betrouwbaarheidsinterval hebben.

 

   

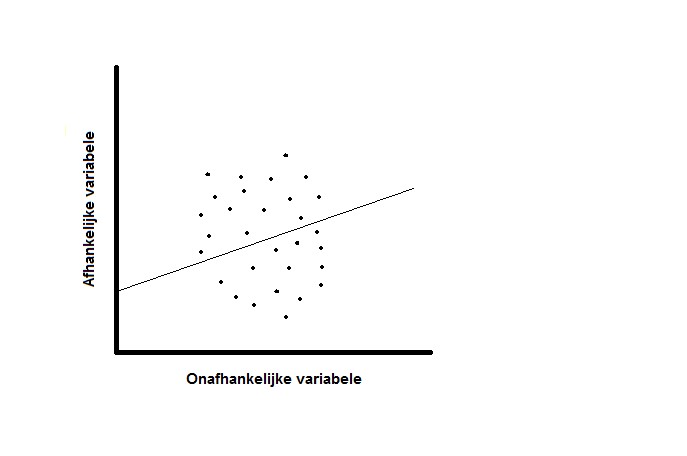
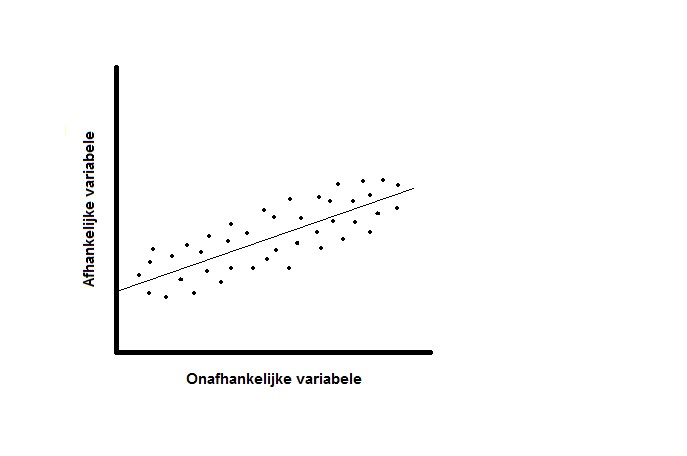
Figuur 2: Zwakke correlatie.                                                                            Figuur 3: Sterke correlatie.

 

 

Voorbeeld:

Om de steekproefgrootte te bepalen vertrok men in de studie van Little (3,4) van een correlatie =0,25 tussen verbale en niet-verbale communicatieve aspecten van de consultatie enerzijds en de perceptie van de patiënt over communicatie en arts-patiëntrelatie anderzijds. De auteurs baseerden zich hiervoor op een gelijkaardige studie (7) waarbij men een Pearson’s correlatiecoëfficiënt vond van r=0,28 met p=0,002 tussen de MISS-score en de patiëntgerichtheid van de arts. Om dit getal beter te kunnen interpreteren gaan we r kwadrateren (r²) en uitdrukken in percentage: (0,28)²x100%=7,8%. We kunnen dan zeggen dat slechts 7,8% van de variatie in MISS-score verklaard kan worden door de patiëntgerichtheid van de arts. Er zijn dus vermoedelijk nog veel andere factoren die de variatie in MISS-score kunnen verklaren. Jammer genoeg geven de auteurs van de studie van Little, naast de ß-regressiecoëfficiënten, geen correlatiecoëfficiënten weer waardoor we de sterkte van de verschillende verbanden niet correct kunnen inschatten (6).

 

Besluit

Terwijl men met correlatie aangeeft hoe sterk het verband is tussen variabelen, probeert men met regressie te achterhalen hoe binnen dat verband de waarde van een afhankelijke variabele gemiddeld zal toenemen of afnemen wanneer de waarde van één of meerdere onafhankelijke (of voorspellende of verklarende) variabelen toeneemt of afneemt. 

 

 

Referenties

1. Sedgwick P. Correlation versus linear regression. BMJ 2013;346:f2686.
2. Sedgwick P. Simple linear regression. BMJ 2013;346:f2340.
3. Little P, White P, Kelly J, et al. Verbal and non-verbal behaviour and patient perception of communication in primary care: an observational study. Br J Gen Pract 2015;65:e357-65.
4. Van Nuland M. Het belang van verbale en non-verbale communicatieve aspecten tijdens de consultatie. Minerva 2016;15(2):35-8.
5. Sedgwick P. Multiple regression. BMJ 2013;347:f4373.
6. Sedgwick P. Correlation. BMJ 2012;345:e5407.
7. Kinnersley P, Stott N, Peters TJ, Harvey I. The patient-centredness of consultations and outcome in primary care. Br J Gen Pract 1999;49:711-6.